Scientists
have long advanced the claim that the human brain is the storage
place for memories and the source of human thinking. But such claims
are speech customs of scientists rather than things they have proven.
There are numerous reasons for doubting such claims. One big reason is that the proteins in synapses have an average lifetime of only a few weeks, which is only a thousandth of the length of time (50 years or more) that humans can store memories. Another reason is that neurons and synapses are way too noisy to explain very accurate human memory recall, such as when a Hamlet actor flawlessly recites 1476 lines. Another general
reason can be stated as follows: the human brain is too slow to
account for very fast thinking and very fast memory retrieval.
Consider the question of memory retrieval. Given a prompt such as a person's name or a very short description of a person, topic or event, humans can accurately retrieve detailed information about such a topic in one or two seconds. We see this ability constantly displayed on the long-running television series Jeopardy. On that show, contestants will be given a short prompt such as “This opera by Rossini had a disastrous premier,” and within a second after hearing that, a contestant may click a buzzer and then a second later give an answer mentioning The Barber of Seville. Similarly, you can play with a well-educated person a game you can call “Who Was I?” You just pick random names of actual people from the arts or history, and require the person to identify the person within about two seconds. Very frequently a person will succeed. We can imagine a session of such a game, occurring in only ten seconds:
John: Marconi.
Mary:
Invented the radio.
John:
Magellan.
Mary:
First to sail around the globe.
John:
Peter Falk.
Mary:
A TV actor.
We can also imagine a visual version of this game, in which you identify random pictures of any of 1000 famous people. The answers would often be just as quick.
The question is: how could a brain possibly achieve retrieval and recognition so quickly? Let us suppose that the information about some person is stored in some particular group of neurons somewhere in the brain. Finding that exact tiny storage location would be like finding a needle in a haystack, or like finding just the right index card in a swimming pool full of index cards. It would also be like opening the door of some vast library with a million volumes and instantly finding the exact volume you were looking for.
There
are certain design features that a system can have that will allow
for very rapid retrieval of information. One of these features is an
indexing system. An indexing system requires a position notation
system, in which the exact position of some piece of information can
be recorded. An ordinary textbook has both of these things. The
position notation system is the page numbering system. The indexing
system is the index at the back of the book. But the brain has
neither of these features. There is nothing in the brain like a
position notation system by which the exact position of some tiny group of neurons can be identified. The brain has no neuron numbers, and a brain
has no coordinate system similar to street names in a city or
Cartesian coordinates in a grid. Lacking any such position notation
system, the brain has no indexing system (something that requires a
position notation system).
So
how is it that humans are able to recall things instantly? It seems
that the brain has nothing like the speed features that would make
such a thing possible. You can't get around such a difficulty by
claiming that each memory is stored everywhere in the brain. There
would be two versions of such an idea. The first would be that each
memory is entirely stored in every little spot of the brain. That
makes no more sense than the idea of a library in which each page
contains the information in every page of every book. The second
version of the idea would be that each memory is broken up and
scattered across the brain. But such an idea actually worsens the
problem of explaining memory retrieval, as it would only be harder to
retrieve a memory if it is scattered all over your brain rather than
in a single little spot of your brain.
We also cannot get around this navigation problem by imagining that when you are asked a question, your brain scans all of its stored information. That doesn't correspond to what happens in our minds. For example, if someone asks me, "Who was Teddy Roosevelt," my mind goes instantly to my memories of Teddy Roosevelt, and I don't experience little flashes of knowledge about countless other people, as if my brain were scanning all of its memories.
When we consider the issue of decoding encoded information, we have an additional strong reason for thinking that the brain is way too slow to account for instantaneous recall of learned information. In order for knowledge to be stored in a brain, it would have to be encoded or translated into some type of neural state. Then, when the memory is recalled, this information would have to be decoded: it would have to be translated from some stored neural state into a thought held in the mind. This requirement is the most gigantic difficulty for any claim that brains store memories. Although they typically maintain that memories are encoded and decoded in the brain, no neuroscientist has ever specified a detailed theory of how such encoding and decoding could work. Besides the huge difficulty that such a system of encoding and decoding would require a kind of "miracle of design" we would never expect for a brain to ever have naturally acquired (something a million times more complicated than the genetic code), there is the difficulty that the decoding would take quite a bit of time, a length of time greater than the time it takes to recall something.
So suppose I have some memory of who George Patton was, stored in my brain as some kind of synapse or neural states, after that information had somehow been translated into synapse or neural states using some encoding scheme. Then when someone asks, "Who was George Patton?" I would have to not only find this stored memory in my brain (like finding a needle in a haystack), but also translate these synapse or neural states back into an idea, so I could instantly answer, "The general in charge of the Third Army in World War II." The time required for the decoding of the stored information would be an additional reason why instantaneous recall could never be happening if you were reading information stored in your brain. The decoding of neurally stored memories would presumably require protein synthesis, but the synthesis of proteins requires minutes of time.
We also cannot get around this navigation problem by imagining that when you are asked a question, your brain scans all of its stored information. That doesn't correspond to what happens in our minds. For example, if someone asks me, "Who was Teddy Roosevelt," my mind goes instantly to my memories of Teddy Roosevelt, and I don't experience little flashes of knowledge about countless other people, as if my brain were scanning all of its memories.
When we consider the issue of decoding encoded information, we have an additional strong reason for thinking that the brain is way too slow to account for instantaneous recall of learned information. In order for knowledge to be stored in a brain, it would have to be encoded or translated into some type of neural state. Then, when the memory is recalled, this information would have to be decoded: it would have to be translated from some stored neural state into a thought held in the mind. This requirement is the most gigantic difficulty for any claim that brains store memories. Although they typically maintain that memories are encoded and decoded in the brain, no neuroscientist has ever specified a detailed theory of how such encoding and decoding could work. Besides the huge difficulty that such a system of encoding and decoding would require a kind of "miracle of design" we would never expect for a brain to ever have naturally acquired (something a million times more complicated than the genetic code), there is the difficulty that the decoding would take quite a bit of time, a length of time greater than the time it takes to recall something.
So suppose I have some memory of who George Patton was, stored in my brain as some kind of synapse or neural states, after that information had somehow been translated into synapse or neural states using some encoding scheme. Then when someone asks, "Who was George Patton?" I would have to not only find this stored memory in my brain (like finding a needle in a haystack), but also translate these synapse or neural states back into an idea, so I could instantly answer, "The general in charge of the Third Army in World War II." The time required for the decoding of the stored information would be an additional reason why instantaneous recall could never be happening if you were reading information stored in your brain. The decoding of neurally stored memories would presumably require protein synthesis, but the synthesis of proteins requires minutes of time.
There is another reason for doubting that the brain is fast enough to account for human mental activity. The reason is that the transmission of signals in a brain is way, way too slow to account for the very rapid speed of human thought and human memory retrieval.
Information travels about in a modern computer at a speed thousands of time faster than nerve signals travel in the human brain. If you type in "speed of brain signals" into the Google search engine, you will see in large letters the number 286 miles per hour, which is a speed of 128 meters per second. This is one of many examples of dubious information which sometimes pops up in a large font at the top of the Google search results. The particular number in question is an estimate made by an anonymous person who quotes no sources, and one who merely claims that brain signals "can" travel at such a speed, not that such a speed is the average speed of brain signals. There is a huge difference between the average speed at which some distance will be traveled and the maximum speed that part of that distance can be traveled (for example, while you may briefly drive at 40 miles per hour while traveling through Los Angeles, your average speed will be much, much less because of traffic lights).
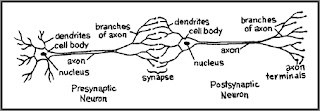
A more common figure you will often see quoted is that nerve signals can travel in the human brain at a rate of about 100 meters per second. But that is the maximum speed at which such a nerve signal can travel, when a nerve signal is traveling across what is called a myelinated axon. Below we see a diagram of a neuron. The axons are the tube-like parts in the diagram below.
The less sophisticated diagram below makes it clear that axons make up only part of the length that brain signals must travel.
There are two types of axons: myelinated axons and non-myelinated axons (myelinated axons having a sheath-like covering shown in blue in the diagram above). According to this article, non-myelinated axons transmit nerve signals at a slower speed of only .5-2 meters per second (roughly one meter per second). Near the end of this article is a table of measured speed of nerve signals traveling across axons in different animals; and in that table we see a variety of speeds varying between .3 meters per second (only about a foot per second) and about 100 meters per second.
But
from the mere fact that nerve signals can travel across myelinated axons at a maximum speed of about 100 meters per second, we are not at all entitled to
conclude that nerve signals typically travel from one region of the brain
to another at 100 meters per second. For nerve signals must also
travel across dendrites and synapses, which we can see in the diagrams above. It turns out that nerve signal transmission is much slower
across dendrites and synapses than across axons. To give an analogy,
the axons are like a road on which you can travel fast, and the
dendrites and synapses are like traffic lights or stop signs that
slow down your speed.
According to neuroscientist Nikolaos C Aggelopoulos, there is an estimate of 0.5 meters per second for the speed of nerve transmission across dendrites (see here for a similar estimate). That is a speed 200 times slower than the nerve transmission speed commonly quoted for myelinated axons. According to Bratislav D. Stefanovic, MD, the conduction speed across dendrites is between .1 and 15 meters per second. Such a speed bump seems more important when we consider a quote by UCLA neurophysicist Mayank Mehta: "Dendrites make up more than 90 percent of neural tissue." Given such a percentage, and such a conduction speed across dendrites, it would seem that the average transmission speed of a brain must be only a small fraction of the 100 meter-per-second transmission in axons.
Besides this “speed bump” of the slower nerve transmission speed across dendrites, there is another “speed bump”: the slower nerve transmission speed across synapses (which you can see in the top “close up” circle of the first diagram above). There are two types of synapses: chemical synapses and electrical synapses. The parts of the brain allegedly involved in thought and memory have almost entirely chemical synapses. (The sources here and here and here and here and here refer to electrical synapses as "rare." The neurosurgeon Jeffrey Schweitzer refers here to electrical synapses as "rare." The paper here tells us on page 401 that electrical synapses -- also called gap junctions -- have only "been described very rarely" in the neocortex of the brain. This paper says that electrical synapses are a "small minority of synapses in the brain.")
We know of a reason why transmission of a nerve signal across chemical synapses should be relatively sluggish. When a nerve signal comes to the head of a chemical synapse, it can no longer travel across the synapse electrically. It must travel by neurotransmitter molecules diffusing across the gap of the synapse. This is much, much slower than what goes on in an axon.
Such a delay may not seem like too much of a speed bump. But consider just how many such "synaptic delays" would have to occur for, say, a brain signal to travel from one region of the brain to another. It has been estimated that the brain contains 100 trillion synapses (a neuron may have thousands of them). So it would seem that for a neural signal to travel from one part of the brain to another part of the brain that is a distance away only 5% or 10% of the length of the brain, that such a signal would have to endure many thousands of such "synaptic delays" requiring a total of quite a few seconds of time.
An average male human brain has about 1300 cubic centimeters. Let's try to calculate the minimum number of synapses that would have to be sequentially traversed in order for a neural signal to travel through a volume of only 1 cubic centimeter (.39 of an inch).
If there are 100 trillion synapses in a brain of 1300 cubic centimeters, then the number of synapses in this volume of 1 cubic centimeter would be roughly 100 trillion divided by 1300, which gives 77 billion. (This page gives an estimate of 418 billion synapses per cubic centimeter, but notes that estimates of synapse density vary; so let's just stick with the smaller number.)
It would be a big mistake to assume that a neural signal would have to sequentially traverse all those 77 billion synapses. To traverse the shortest path across this area, the signal would have to merely pass through a number of synapses that is roughly the cube root of the total number of synapses in this volume (the number that you would have to multiply by itself three times to get the total number of synapses in this volume). Similarly, if we imagine a ball with 64 equally spaced connected nodes, including nodes in the center, something rather like the ball shown below, then it is clear that the shortest path between any one node at the outer edge of the ball to another node on the opposite end of the ball would require that you traverse a number of nodes that is at least the cube root of 64, which is 4.
So to roughly compute the shortest series of synapses that would have to be traversed for a brain signal to travel though this 1 cubic centimeter volume, we can take the cube root of 77 billion (the number that multiplied by itself three different times equals 77 billion). The cube root of 77 billion is 4254. So it seems that to traverse the shortest path through a volume of 1 cubic centimeter containing 77 billion synapses, traveling a distance of about 1 cubic centimeter, a neural signal would have to pass sequentially through a path containing at least 4000 different synapses (along with other neural elements such as dendrites).
To calculate how long this traversal would take across a 1 cubic centimeter region of the brain, considering only the dominant delay factor of synaptic delays, we can simply multiply this number of 4000 by the synaptic delay (the time needed for the signal to cross a single synaptic gap). Using the smallest estimate of the synaptic delay (an estimate from 1965 of about .5 millisecond), and ignoring the more recent year 2000 estimate of 2.29 milliseconds for the synaptic delay, this gives us a total time of 4000 multiplied by .5 millisecond. This gives us a total time of two seconds (2000 milliseconds) for how long it would take a nerve signal to travel across one cubic centimeter of brain tissue. The velocity of nerve signal speed we get from this calculation is a speed of less than 1 centimeter per second (it's actually a speed of a half a centimeter per second).
Take careful note that this speed is more than 10,000 times slower than the "100 meters per second" figure that is given by some experts when they are asked about how fast a brain signal travels. Such an expert answer is very misleading, because it only calculates the fastest speed that a nerve signal can travel inside the brain, while it is traveling through the fastest tiny parts of the brain (myelinated axons), not the average speed of such a brain signal as it passes through different types of brain tissue and many different synapses. It turns out that because of the "speed bump' of synaptic delays, the average speed of a nerve signal traveling though the brain should be about 20,000 times slower than "100 meters per second" -- a slowpoke speed of about a half of a centimeter per second. That's half the maximum speed at which a snail can move. If I had used the year 2000 estimate of the synaptic delay (2.29 milliseconds), I would have got a speed estimate for brain signals that is only about .125 centimeters per second, which is one eighth the speed of a moving snail.
This calculation is of the utmost relevance to the question of whether the brain is fast enough to account for extremely rapid human thinking and instantaneous memory retrieval. Based on what I have discussed, it seems that signal transmission across regions of the brain should be very slow -- way too slow to account for very fast thinking and instantaneous recall and recognition.
Many a human can calculate as fast as he or she can recall. For example, the Guinness world record web site tells us, "Scott Flansburg of Phoenix, Arizona, USA, correctly added a randomly selected two-digit number (38) to itself 36 times in 15 seconds without the use of a calculator on 27 April 2000 on the set of Guinness World Records in Wembley, UK." Such speed cannot be explained as the activity of a brain in which signals literally move at a less than a snail's pace.
To give another example, In 2004 Alexis Lemaire was able to calculate in his head the 13th root of this number:
85,877,066,894,718,045, 602,549,144,850,158,599,202,771,247,748,960,878,023,151, 390,314,284,284,465,842,798,373,290,242,826,571,823,153, 045,030,300,932,591,615,405,929,429,773,640,895,967,991,430,381,763,526,613,357,308,674,592,650,724,521,841,103,664,923,661,204,223
In only 77 seconds, according to the BBC, Lemaire was able to state that it is the number 2396232838850303 which when multiplied by itself 13 times equals the number above. Here we have calculation speed far beyond anything that could be possible if calculation is done by a brain in which signals travel at less than a snail's pace.
Echoing part of what I have said here, a textbook says "the cumulative synaptic delay may exceed the propagation time along the axons." But why aren't scientists more explicit, by telling us that this cumulative synaptic delay will actually exceed the propagation time along the axons by a factor of more than 1000, leading to "snail's pace" brain signals? Another source vaguely tells us that "cumulative synaptic delay would affect the speed of information processing at every level of cognitive complexity" without mentioning what a crippling effect this would be if our brains were doing thinking and recall.
I may note whenever a neuroscientist answers a question such as "how fast do brain signals travel" by mentioning only the fastest rate at which a brain signal can travel through the fastest little parts of the brain (through a myelinated axon), such as neuroscientists typically do, such an answer is either deceptive or very clumsy. It's like answering the question "how fast can you travel across Manhattan" by citing the maximum speed limit on any Manhattan cross-street such as 42nd Street, without considering all the delays caused by traffic lights. Synaptic delays are comparable to traffic light delays, and they are a factor that must be calculated when realistically considering how fast a brain signal typically travels inside the brain.
It is interesting that both this 1979 scientific paper and this 2008 scientific paper estimate the number of synapses in the human cortex as being about a billion per cubic millimeter, which equals a trillion per cubic centimeter. This is 10+ times greater than the 77 billion per cubic centimeter figure I was using above. The more synapses, the more speed bumps, and the slower the brain signal. If I had done the brain speed calculation specifically for cortex tissue (the supposed center of higher thought), the calculation would have come up with a brain signal speed very much slower than the half a centimeter per second result that was reached.
To sum up, we have several gigantic reasons for thinking that brains must be too slow to account for instantaneous recall:
(1) Finding the exact little spot where a memory was stored would be like finding a needle in a haystack, given the lack of any indexing system or position coordinate system in the brain.
(2) Decoding stored memories from encoded neural states would take additional time that would make neural memory recall much less than instantaneous.
(3) The "snail's pace" speed of brain signals (greatly slowed by synaptic delays) would prevent an instantaneous recall of memories and stored information such as humans often have.
The slowness of the brain is one of many neuroscience reasons for believing that the brain cannot be the storage place of our memories, and cannot be the source of our thinking and consciousness. Human mentality must be primarily a psychic or spiritual or non-biological reality rather than a neural reality.
I can imagine various ways in which a person could try to rebut some of the argumentation in this post, Someone could simply say that we know that signals must travel very fast in a brain, because humans are able to recall things instantly or recognize things instantly. But we do not at all know that recognition or recall are actually effects produced by the brain, and we have good reasons for doubting that they are (such as the short lifetimes of synapse proteins and the fact that the high noise levels in brains and synapses is incompatible with the fact that humans such as Hamlet actors can flawlessly recall very large bodies of memorized information). So we cannot use the speed of recognition or recall to deduce the speed of brain signals.
Another way you could try to rebut this post would be to cite some expert who estimated how fast signals move about in a brain. But further analysis would generally show that such an estimate was not derived from a calculation of all the low-level factors (such as synaptic delay) affecting the speed of brain signals, but was simply a calculation based on the assumption that brains must pass about signals at the speed at which humans recognize or recall things or respond to things. We cannot use such circular reasoning or "begging the question" when considering this matter. The only intelligent way to calculate the speed of a brain signal is to do a calculation based on low-level things (such as synaptic delays) that we definitely know, rather than starting out making grand assumptions about the mind and brain that are unproven and actually discredited by the very low-level facts (such as the length of synaptic delays) that should be examined.
Although neuroscientists typically claim that synapses are where memories are stored in the brain, there are four ways in which the characteristics of synapses are telling us that thinking and memory is not brain-caused:
(1) Synapses show no signs of having stored information, and their main structural feature (the disorganized little blob or bag that is the synaptic knob or head) seems like pretty much the last type of structure we'd expect to see in something storing information for decades.
(2) Synapses are unstable units undergoing spontaneous remodeling, and synapses consist of proteins with average lifetimes of only a few weeks, only a thousandth of the maximum length of time that humans store memories.
(3) Synapses are very noisy, so noisy that one expert tells us that a signal passing through a synapse "makes it across the synapse with a probability like one half, or even less," making synapses unsuitable as reliable transmitters of memory information that humans such as Wagnerian tenors can recall abundantly with 100% accuracy. Given such noise levels, which would seem to have the effect of rapidly extinguishing brain signals, there would seem to be good reason for suspecting that it is effectively impossible for brain signals to travel more than a centimeter or an inch without vanishing or becoming mere tiny traces of their original strength.
(4) The most common type of synapse is slow, and although the synaptic delay in a single synapse is only about a millisecond, when we calculate the cumulative synaptic delay we find that brain signals must be slower than a snail's pace, way too slow to explain instantaneous recall and fast thinking.
In fact, if some designer of the human body had specifically designed something to tell us (by its characteristics) that our brains cannot be the source of our fast thinking and instantaneous memory, it's rather hard to imagine anything that would do a better job of telling us that than our signal-slowing, very noisy, unstable synapses. Our synapses are telling us (by their characteristics) that thinking and memory is not brain-caused, but our neuroscientists (trapped in ideological enclaves of dogma and reigning speech customs) aren't listening to what our synapses are telling us.
Postscript: I may note that you do not get a much faster estimate for the speed of brain signals if you calculate the speed from one neuron to the nearest neuron, rather than the speed through a cubic centimeter. The speed is the same snail's pace I have calculated, because the signal will always have to pass through synapses that are the dominant slowing factor.
There is an entirely different method you could use to calculate the speed of signals inside the brain, using not estimates of the number of synapses per cubic centimeter, but instead the average distance between neurons. This paper mentions an average distance of about 26 micrometers between neurons in a rat cortex, and it says, "we believe that the parameter of 26 µm [micrometers] average distance between neurons is also a valid assumption in the human brain." I assume that by "average distance between neurons" this source means the average distance between two adjacent neurons. Below are some calculation figures that we get if we use this average distance figure, and we use a synaptic delay estimate that is about the average of the .5 millisecond and 2.29 millisecond estimates quoted above.
| Average distance between neurons in micrometers | 26 |
| This distance in centimeters | 0.0026 |
| Synaptic delay in milliseconds | 1 |
| Time needed to cross distance above (in seconds), considering only the synaptic delay | .001 |
| Total distance that could be traversed by a brain signal in a second | 1000*0.0026 centimeter=2.6 centimeter |
| Signal speed between adjacent neurons in centimeters per second | 2.6 |
Using this method, we get a result in the same ballpark as the result calculated by my first method. The first method found that brain signals travel at a rate of about .5 centimeters per second, and this method finds that brain signals travel at about 2.6 centimeters per second, which is about an inch per second. Either way, this speed is way too slow to account for instantaneous recall and very rapid thinking.
A most-realistic estimate of brain signal speed would also take into account two other factors ignored in the calculations above (and also ignored by neuroscientists when discussing the speed of brain signals):
(1) The noise in synapses, and the fact that in the cortex, signal transmission across synapses is highly unreliable. A scientific paper says, "In the cortex, individual synapses seem to be extremely unreliable: the probability of transmitter release in response to a single action potential can be as low as 0.1 or lower." Considered over a large section of brain tissue, this unreliability would be equivalent to a big additional slowing factor, and might well lead to speed estimates much lower than I have made here.
(2) Synaptic fatigue, a temporary inability of the head or vesicle of a synapse to send a signal, because of a depletion of neurotransmitters. Referring to synaptic fatigue, one paper states the following:
By contrast, following neurotransmission, synaptic vesicle membranes are internalized within seconds, and the recycled synaptic vesicles can be reloaded with neurotransmitter within 1–2 minutes.
This paper mentions a much shorter "timescale of vesicle recovery" of 800 milliseconds, but even that would be a large slowing factor, making it all the more unlikely that brain signals inside the cortex can regularly travel about at much more than about a centimeter per second.
There are two other factors I didn't mention in my original post, both tending to further slow the speed of a signal from one end of the brain to another:
(1) Tortuosity: the fact that a shortest path between two different brain areas is typically a sinuous, snake-like path rather than a straight line (tortuosity is the technical term for such a thing).
(2) Folding of cerebral tissue: the surface area of cerebral tissue is much larger than you might think by looking at the top of a head; and a brain signal can't travel a straight line between these folds.
So below is a list of all of the factors that must be considered when considering the true speed of signals between two opposite areas of the brain:
(1) The speed of transmission through dendrites, which can be 200 or more times slower than the "100 meters per second" estimate based on transmission through axons.
(2) Synaptic delays, which end up being a huge slowing factor because so many synapses must be traversed.
(3) Synaptic unreliability or noise, the fact that a signal is often transmitted with only between 10% to 50% likelihood, a factor that is typically ignored but which has a huge impact on effective speed.
(4) Synaptic fatigue, the fact that a synapse will so often need a rest period after firing, a period that can be more than a minute.
(5) Tortuosity, the fact that nerve signals must travel through sinuous paths that are not straight lines.
(6) Folding of cortex tissue, a further slowing factor.
Every one of these factors is ignored by 95% of discussions of brain signal speed in the popular press.
A 2011 LiveScience.com article is entitled "Speed of Brain Cell Chatter Clocked for the First Time." Buried within the article is a fact that corroborates what I have said in this post. The article discusses an experiment in which scientists clocked signal speed in mouse brains, by tagging neurotransmitters with a fluorescent protein. The article reports, "On average, it takes about five seconds for the cells to collect up the neurotransmitters and this timeframe didn't vary much between a cell's different synapses." This is the only speed figure given by the article. Since the article was talking about a mouse brain (no larger than about two centimeters across), this is exactly the "snail's pace" signal transmission rate that I have claimed in this post, a pace of roughly one centimeter per second.
A 2020 paper was entitled "Kilohertz two-photon fluorescence microscopy imaging of neural
2 activity in vivo." It used some fancy new technology to clock the speed of brain signals in a living mouse. Supplementary Figure 5 of the paper refers to a calcium propagating speed of about 25 microns per second, which is a very slow speed of only 0.0025 centimeters per second. If human brain signals travel at such a speed, the brain must be thousands of times too slow to account for instant recall.
The paper here clocks the speed of seizures in zebrafish, and finds them to be a maximum of 10.5 millimeters per second, a speed of 1.05 centimeters per second. This is almost exactly the same as estimate I give in the visual above: the rough estimate of only 1 centimeter per second for brain signals. The paper here lists a speed of only about 1 millimeter per second for seizures in the human brain, saying, "Seizures propagate slowly to connected areas with speeds on the order of 1 mm/s." There is no reason to think that some hypothetical brain signals involved in thinking would occur much faster than seizures.
A 2015 paper describes the speed of the transmission of various brain signals, without considering synaptic slowing factors. It lists these brain signal speeds:
"Interestingly, signal propagation speeds in various conditions are similar (~0.1 m/s). Neural spikes generated by 4-aminopyridine (4-AP) travel with a longi-tudinal speed of 0.09/0.03 m/s along the CA3 region (Kiblerand Durand, 2011), whereas in the presence of picrotoxin, synchronous firing events propagate longitudinally at 0.14 /0.04m/s (Miles et al., 1988). High K+-, low Mg2+-, and zero-Ca2+- triggered spikes again exhibit speeds of 0.07-0.1 m/s, 0.1– 0.15m/s, and 0.04 – 0.15 m/s, respectively (Haas and Jefferys, 1984;Quilichini et al., 2002;Liu et al., 2013). In normal tissue, theta oscillations travel with a speed of 0.08 – 0.107 m/s in the hip-pocampus of living rodent rats (Lubenov and Siapas, 2009),whereas carbachol-induced theta oscillations travels with a speed of 0.119 m/s along the CA1 cell layer and a 0.141 m/s along the CA3 cell layer (Cappaert et al., 2009). Together, it is clear that 0.1m/s is a common propagation speed regardless of experimental models...Other propagation mechanisms, such as extracellular ionic transients and axonal conduction mechanisms, have very different propagation speeds (0.0004 – 0.008 m/s for K+ diffusion and 0.3– 0.5 m/s for axonal conduction, Miles et al., 1988;Lian et al., 2001;Francis et al., 2003;Meeks and Mennerick, 2007;Jensen, 2008;Kibler et al., 2012)."
Given such numbers, my estimate above for an average brain signal speed transmission of only about 1 centimeter per second seems roughly correct. Some of the speeds quoted above are about five to ten times faster than my estimate, but the estimate for K+ diffusion (potassium diffusion) is much slower than my estimate. Most of the numbers quoted above are about 1000 times slower than the incorrect "100 meters per second" figure often given for brain signal speed. The speeds quoted above are "fastest time" quotes that don't consider all the slowing produced by cumulative synaptic delays and other slowing factors.
The 2021 paper "Brain Activity Fluctuations Propagate as Waves Traversing the Cortical Hierarchy" mentions an average speed of about 10 millimeters per second, which is very close to the rough estimate I give above of a brain signal speed of about 1 centimeter per second (10 millimeters per second is the same as 1 centimeter per second). We read this: "The top-down propagations (N = 8519) and bottom-up propagations (N = 18 114) were found to account for 9.08% and 19.7% of the total scanning time, respectively, with an average speed of 13.45 ± 7.78 and 13.74 ± 7.51 mm/s (mean ± SD), respectively."
Then there's the fact that only about half of the axons in the cortex of the brain are the faster myelinated type of axon (as discussed in the scientific paper here). The other half of the axons are very much slower unmyelinated axons. The diagram below schematically depicts the "speed bumps" in the brain. Such "speed bumps" vastly outnumber the fastest parts (myelinated axons). The result is that brains cannot explain phenomena such as instant recall upon hearing a famous person's name and very fast reading with good understanding of what is read.




No comments:
Post a Comment