Exceptionally Fast Thinking Cannot Be Explained by Slow Brains Like We All Have

Information travels about in a modern computer at a speed thousands  of times faster than nerve signals travel in the human brain. If you type in "speed of brain signals" into the Google search engine, you will see in large letters the number 286 miles per hour, which is a speed of 128 meters per second. This is one of many examples of a dubious claim which sometimes pops up in a large font at the top of the Google search results. The particular number in question is an estimate made by an anonymous person who quotes no sources, and one who merely claims that brain signals "can" travel at such a speed, not that such a speed is the average speed of brain signals. There is a huge difference between the average speed at which some distance will be traveled and the maximum speed that part of that distance can be traveled. For example, while you may briefly drive at 40 miles per hour while traveling through Manhattan or Paris, your average speed will be much, much less because of traffic lights and stop signs. 

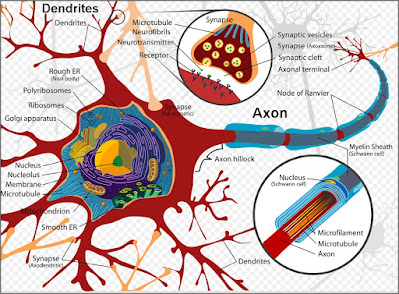
A speed such as about 100 meters per second is the maximum speed at which such a nerve signal can travel, when a nerve signal is traveling across what is called a myelinated axon. Below we see a diagram of a neuron. The axons are the tube-like parts in the diagram below.

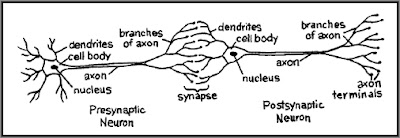
The less sophisticated diagram below makes it clear that axons make up only part of the length that brain signals must travel.

There are two types of axons: myelinated axons and non-myelinated axons (myelinated axons having a sheath-like covering shown in blue in the diagram above). According to this article, non-myelinated axons transmit nerve signals at a slower speed of only .5-2 meters per second (roughly one meter per second).  We are told that higher thought comes from the cortex of the brain. But most of the axons in the cortex are not myelinated. 

Nerve signals must also travel across dendrites and synapses, which we can see in the diagrams above. It turns out that nerve signal transmission is much slower across dendrites and synapses than across axons. To give an analogy, the axons are like a road on which you can travel fast, and the dendrites and synapses are like traffic lights or stop signs that slow down your speed.

According to neuroscientist Nikolaos C Aggelopoulos, there is an estimate of 0.5 meters per second for the speed of nerve transmission across dendrites (see here for a similar estimate). That is a speed 200 times slower than the nerve transmission speed commonly quoted for myelinated axons. According to Bratislav D. Stefanovic, MD, the conduction speed across dendrites is between .1 and 15 meters per second. Such a speed bump seems more important when we consider a quote by UCLA neurophysicist Mayank Mehta: "Dendrites make up more than 90 percent of neural tissue."  Given such a percentage, and such a conduction speed across dendrites, it would seem that the average transmission speed of a brain must be only a small fraction of the 100 meter-per-second transmission in myelinated axons. 

Besides this “speed bump” of the slower nerve transmission speed across dendrites, there is another “speed bump”: the slower nerve transmission speed across synapses (which you can see in the top “close up” circle of the first diagram above). There are two types of synapses: chemical synapses and electrical synapses. The parts of the brain allegedly involved in thought and memory have almost entirely chemical synapses. (The sources here and here and here and here and here refer to electrical synapses as "rare."  The neurosurgeon Jeffrey Schweitzer refers here to electrical synapses as "rare."  The paper here tells us on page 401 that electrical synapses -- also called gap junctions -- have only "been described very rarely" in the neocortex of the brain. This paper says that electrical synapses are a "small minority of synapses in the brain.")

There is a scientific term used for the delay caused when a nerve signal travels across a synapse. The delay is called the synaptic delay. According to this 1965 scientific paper, most synaptic delays are about .5 milliseconds, but there are also quite a few as long as 2 to 4 milliseconds. A more recent (and probably more reliable) estimate was made in a 2000 paper studying the prefrontal monkey cortex. That paper says, "the synaptic delay, estimated from the y-axis intercepts of the linear regressions, was 2.29" milliseconds. It is very important to realize that this synaptic delay is not the total delay caused by a nerve signal as it passes across different synapses. The synaptic delay is the delay caused each and every time that the nerve signal passes across a synapse. 

Such a delay may not seem like too much of a speed bump. But consider just how many such "synaptic delays" would have to occur for, say, a brain signal to travel from one region of the brain to another. It has been estimated that the brain contains 100 trillion synapses (a neuron may have thousands of them).  So it would seem that for a neural signal to travel from one part of the brain to another part of the brain that is a distance away only 5% or 10% of the length of the brain, that such a signal would have to endure many thousands of such "synaptic delays" requiring a total of quite a few seconds of time. 

Humans can recall information instantly given a one-word prompt, but such an ability is inexplicable given the physical limitations of brains. We know the type of things that make instant data retrieval possible in computers: features such as indexing, sorting and addressing. The brain has no such features. Given its physical nature, trying to remember anything by retrieving information from a brain would be like trying to find a needle in a haystack. 

Because of all of these reasons, it seems that brains are far too slow to explain normal fast thinking and normal fast recall.  Human recall of learned information typically occurs instantaneously.  We see this on the show "Jeopardy," where contestants typically give correct answers within a second or two after being prompted about obscure information.  For example, when read the prompt "The battle that had a fateful mistake known as Pickett's Charge," contestants within 1 second may start to answer "What is Gettysburg?" And if I ask some old people "Which US president succeeded Jimmy Carter?" it will take only a second before I hear an answer of "Reagan."

Humans can also think very fast. There are many historical cases of math prodigies that could calculate with incredible speed and accuracy.  The passage below describes the blazing fast calculation powers of Zerah Colburn:

"This child undertook, and completely succeeded in, raising the number 8 progressively up to the sixteenth power. And in naming the last result, viz.: 281, 474, 976, 710, 656, he was right in every figure. He was then tried as to other numbers consisting of one figure, all of which he raised (by actual multiplication, and not by memory) as high as the tenth power, with so much facility and dispatch that the person appointed to take down the results was obliged to enjoin him not to be so rapid. With respect to numbers consisting of two figures, he would raise some of them to the sixth, seventh and eighth power....He was asked the square root of I06,929, and before the number could be written, he immediately answered, 327. He was then required to name the cube root of 268,336,125, and with equal facility and promptness he replied, 645. Various other questions of a similar nature, respecting the the roots and powers of very high numbers, were proposed by several of the gentlemen present, to all of which he answered in a similar manner. One of the party requested him to name the factors which produced the number 247,483: this he immediately did by mentioning the numbers 941 and 263 — which, indeed, are the only two numbers that will produce it...One of the gentlemen asked him how many minutes there were in forty-eight years; and before the question could be written down, he replied 25,228,800; and instantly added that the number of seconds in the same period was 1,513,728,000."

The passage below tells us about the incredibly fast calculation speed of  Jacques Inaudi, born in 1867:

"In his exercises of mental calculation, Mr. Inaudi is remarkable in two particulars, the complexity of his work and the rapidity with which he completes it. The greater number of questions given to him contain many figures. He will add in his head two numbers consisting of twelve figures each ; he will multiply two numbers composed of eight figures ; he will tell how many seconds there are in any promiscuously chosen number of years, months, days, and hours. These operations demand that he shall hold in his memory the exact problem and the partial solutions up to the time when the complete result is found. For such a considerable work as this, Mr. Inaudi gives an extremely short time, so short, indeed, as sometimes to produce the illusion of instantaneity. The following paragraph has been published concerning him. ' He adds in a few seconds seven numbers of eight or ten figures each; he subtracts one number from another each composed of twenty-one figures in less than a minute; he finds as rapidly the square root or the cube root of numbers consisting of from eight to twelve figures, if these numbers are perfect squares or cubes; it takes a little longer for the last-named work if there is a remainder necessitating a fractional part to the answer. He finds with incredible celerity the sixth or the seventh root of large numbers. He will multiply or divide in less time than it takes him to announce the results. As an example of what has been said, we give the following: He was asked the number of seconds in 18 years, 7 months, 21 days and 3 hours. The response was given in thirteen seconds."

Page 250 of the May 21, 1880 edition of The Spiritualist has a story about Jacques Inaudi, spelling his name Inodi.  We read this about the boy who was then a mere adolescent:

"Persons who desire to know the number of minutes and seconds that they have lived do not puzzle him in the least; almost instantaneously he gives the answer. That which appeared most to fatigue him was simple multiplication, rather a long sum, it is true. He was asked to multiply 78,965,428 by 56,789. Not having these numbers before his eyes, and moreover, not being able to read, it was necessary to repeat them two or three times, until having remembered them, he could repeat them alone himself. A moment after, he dictated this exact and long product, 4,484,367,690,692, not however, without having thought (cherehe) a little, with an evidently laborious effort, which proves that he is not aided by mediumship.”

In the twentieth century the legendary mathematician John von Neumann was famous for his lightning-fast problem solving abilities. When he was six years old, he could divide two eight-digit numbers in his head. The wikipedia.org article on him mentions some of the greatest thinkers of his time saying that von Neumann was the fastest thinker they had ever met. We read this story about a problem posed to von Neumann:

"Two bicyclists start 20 miles apart and head toward each other, each going at a steady rate of 10 mph. At the same time a fly that travels at a steady 15 mph starts from the front wheel of the southbound bicycle and flies to the front wheel of the northbound one, then turns around and flies to the front wheel of the southbound one again, and continues in this manner till he is crushed between the two front wheels. Question: what total distance did the fly cover? ...When the question was put to von Neumann, he solved it in an instant, and thereby disappointed the questioner: 'Oh, you must have heard the trick before!' 'What trick?' asked von Neumann, 'All I did was sum the geometric series.' "

Neelakantha Bhanu Prakash has been called the world's fastest calculator, and can do things such as multiply 869,463,853 times 73 correctly in only 26 seconds, giving an answer of 63,470,861,269. This is despite having a very serious head injury which required 86 stitches, and left him with a prominent scar on his forehead. According to the Guinness Book of World Records, "Scott Flansburg of Phoenix, Arizona, USA, correctly added a randomly selected two-digit number (38) to itself 36 times in 15 seconds without the use of a calculator on 27 April 2000 on the set of Guinness World Records in Wembley, UK." 

A scientific paper tells us this about the autistic savant Daniel Tammet:

"DT [Daniel Tammet] speaks 10 languages, including Estonian and Finnish, has invented his own language (Manti) and learnt Spanish in one weekend. He performs mathematical calculations at lightning speed, including multiplying six-digit numbers together. He commented that 31, 19, 79 and 1979 are all prime numbers, an indication of how he sees patterns in numbers very rapidly. As mentioned earlier, as part of a formal competition he recited Pi to 22,514 decimal paces, earning the title of European champion."

The book Bright Splinters of the Mind  by Beate Hermelin is about autistic savants, those with special skills despite seeming to be largely defective in some areas of mental functioning.  On page 63 of the book we read this about a gifted subject: "Christopher can understand, talk, read, write and translate from Danish, Dutch, Finnish, French, German, Greek, Hindi, Italian, Norwegian, Polish, Portuguese, Russian, Spanish, Swedish, Turkish and Welsh." On page 300 the book mentions twins who could recall up to 300 digits. On page 17 the author reports being introduced to a 13-year-old boy who immediately asks him his birthday:

"When I told him it was 7 August, he said instantly, 'That was on a Wednesday in 1940, and in 2004 it will be on a Wednesday again.' I was stunned, and of course had no idea whether he was right. (He was!)" 

Quite a few such accounts of instantaneous human calendar calculation  are found in this book and a book by Darold A. Treffert. Below are statements made by Treffert in his very interesting book Extraordinary People: Understanding Savant Syndrome:

• In 1788 the slave Thomas Fuller (who could neither read nor write) was asked "How many seconds has a man lived who is 70 years, 17 days and 12 hours old?"  90 later seconds Fuller gave a correct reply of 2,210,500,800. His obituary stated that "he could give the number of months, days, weeks, hours, minutes, and seconds in any period of time that any person chose to mention, allowing in his calculation for all the leap years that happen in the time."
• A Dr. J. Langdon Down described a 12-year-old boy who could multiply any three numbers by any other three numbers, as quickly as Down could write the six numbers on paper.
• A Dr. Alfred F. Tredgold mentioned a person who could give the square root of any four digit number in an average of four seconds, and who could give the cube root of any six-digit number in about six seconds. He said that when the same person "was asked about how many grains of corn there be in any one of 64 boxes, with 1 in the first, 2 in the second, 4 in the third, 8 in the fourth, and so on, he gave answers for the fourtheenth (8,192), for the eighteenth (131,072), and the twenty-fourth (8,388,608) instantaneously, and he gave the answer for the forty-eighth box (140,737,488,355,328) in six seconds," and that he "also gave the total in all 64 boxes correctly (18,446,734,073,709,551,615) in forty-five seconds."
• A blind boy named Fleury was of such low intelligence he had to be institutionalized, but he could calculate 2 to the 30th power (1,073,741,824) in only 40 seconds, and could calculate the cube root of 465,484,375 (which is 775) in 13 seconds.
• A pair of twins named George and Charles (born three months prematurely) could do calendar calculations with blazing speed. We read this: "Give them a date and they can give you day of the week over a span of 80,000 years, 40,000 backward or 40,000 forward." Also, we read that if you "ask them to name in which years in the next 200 (or any 200) Easter will fall on March 23," then they "will name those years with lightning rapidity, faster than a computer and just as accurately." This seems all the more impressive when you consider that the rules for when Easter will occur in a particular year are quite complicated. In the same chapter we read about other people who could do calendar calculations with blazing speed.
• A subject ND was tested using "randomly selected calendars from the last 300 years with the help of a computer program," being asked  the "weekdays of randomly selected calendar dates."  He "correctly answered all questions with a mean delay of 1 s [one second]" which means he instantly answered correctly all the questions such as which day of the week was October 23, 1745. 

Treffert's book is filled with cases like these: cases of people who think way, way faster than should be possible with a brain such as humans have, and cases of people who remember way, way better than should be possible with brains such as ours, having none of the main characteristics of manufactured information storage systems such as computers. Many of these people had severe brain damage. But Treffert failed to put two and two together in this matter. On page 207-208 he asks some questions that should raise doubts about claims of neural memory storage. We read this set of questions about human memory:

"Is storage electrical? If so, then why aren't memories permanently destroyed during an epileptical seizure, which is truly an electrical storm in the brain -- as can be witnessed by watching an EEG during a seizure? Or, if storage is electrical, why aren't memories permanently affected when a patient receives electroconvulsive therapy (ECT), during which time an electrical current is passed through the brain ? If storage is electromagnetic in the same manner that storage of 'memories' on tape or storage of data on a computer is, then why isn't memory permanently affected by a nuclear magnetic resonance (NMR) brain scan, during which the brain is subjected to tremendous magnetic fields? Try that with some tapes or disks. If storage is an actual physical storage, like grooves on a phonograph disk, why isn't there some clear evidence of that process in microscopic examination of the brain?" 

I wish this quote could be posted on the wall of every neuroscientist. Alas, Treffert failed to ponder the implications of his own questions. On page 208, he says "These, and many more, are questions I guess we will need to leave for the future"; and then in the rest of the book he just keeps spouting conventional neuroscience dogmas about memories storing brains. Treffert should have concluded from his own questions and the case histories he reported (often involving heavily brain-damaged people with blazing fast minds or exceptionally powerful memories) that the brain is not the source of human minds, and not the storage place of human memories. 

To find cases of human mental performance that should be utterly impossible given the physical limitations of the brain, you do not need to delve into the literature documenting paranormal phenomena (although doing that will yield a huge number of such cases). You can merely search for the most remarkable cases of mental performance that are not disputed. Besides searching for cases of exceptionally fast thinking, you can search for cases of exceptional memory. Below is a quote from page 53 of the book The Mind and Beyond published by Time-Life Books:

"As reported in the 1990 edition of the Guinness Book of World Records, in 1967, one Mehmed Ali Halici of Turkey recited from memory 6,666 verses of the Koran in six hours. And in 1989, Englishman Tony Power memorized in correct order a random sequence of thirteen packs of shuffled playing cards – 676 cards in all – after looking at them only once. But the world record for a single eidetic memory feat may be held by Bhandanta Vicitasara of Rangoon, Burma who in 1974 correctly recited from memory 16,000 pages of Buddhist canonical texts."

Mehmed Ali Halici's recitation rate was so fast it was faster than a normal person speaking as fast as he can. This was six hours of memory recall at a rate that was basically instantaneous. A hundredth of such speed would have been impossible given a brain with all the speed limits mentioned above.  The fast recall of a single page of memorized text is not explainable under the dogmas of neuroscientists, who have no credible explanation as to how a brain could store a single page of text, no explanation of how memories could be preserved for years, and no explanation of how memorized information could be instantly retrieved in brains lacking any of the things that make fast recall possible (such as addressing, sorting and indexes). Not one single word has ever been found stored in brain tissue by examining brain tissue. 

There is no neuroscientist in the world who can give a detailed credible explanation of how a human brain could even store the mere phrase "my dog has fleas," giving a precise worked example showing how each one of those characters could be stored in a brain. When neuroscientists talk about memories being stored by "alteration in connection patterns" or "synapse strengthening," they are engaging in mere hand waving. As Treffert asked, "If storage is an actual physical storage, like grooves on a phonograph disk, why isn't there some clear evidence of that process in microscopic examination of the brain?" The very likely answer is: because brains do not store information humans memorize. 

If Neuroscientists Acted Like Cosmologists, They Might Say You Have an Invisible "Dark Brain"

From a sociological perspective the academia tribe of neuroscientists has many similarities with the academia tribe of cosmologists (scientists who study the universe as a whole). Both are belief communities zealously committed to advancing unproven dogmas. The unproven dogmas of the neuroscientist belief community include the dogma that the brain is the source of the mind (or the same thing as the mind), and the belief that memories are stored in the brain. The unproven dogmas of the cosmologist belief community include a belief in primordial cosmic inflation (the idea that the universe underwent exponential expansion for an instant at its beginning), the dogma of dark matter and the dogma of dark energy. 

But there is one important difference between these belief communities: cosmologists have shown a willingness to postulate the existence of invisible realities to try to make up for things they cannot explain, but neuroscientists refuse to do such a thing, clinging to a "the brain explains it all" dogma that dramatically fails to account for observational reality.  To explain this difference, let me describe why cosmologists claim that there is dark matter and dark energy. 

What led to the belief in dark matter was the discrepancy shown in the visual below. Astronomers thought that the rotation velocity of stars (the speed at which they rotate around the center of the galaxy) should decrease the more the stars are located from the center of a galaxy (which would be the behavior shown by the blue line below). But instead stars rotated around the center of their galaxy with the speed shown in the red line. 

Unable to account for such observations by anything they knew of in the visible universe, cosmologists postulated the existence of an invisible: "dark matter" existing in greater amounts than ordinary matter. Something rather similar led to cosmologists postulating the idea of dark energy. Scientists seemed to observe the universe expanding at an accelerating rate they could not account for by using only the known matter and energy in the universe. To account for the rate of the universe's expansion, scientists began to postulate that most of the universe's mass-energy exists in the form of a mysterious "dark energy" that acts as a "cosmological constant," a kind of repulsive force. 

A scientific web site explains dark energy like this (failing to see the irony of matter-of-factly making an exact "72%" claim about a merely hypothetical substance):

"Dark Energy is a hypothetical form of energy that exerts a negative, repulsive pressure, behaving like the opposite of gravity. It has been hypothesised to account for the observational properties of distant type Ia supernovae, which show the universe going through an accelerated period of expansion. Like Dark Matter, Dark Energy is not directly observed, but rather inferred from observations of gravitational interactions between astronomical objects. Dark Energy makes up 72% of the total mass-energy density of the universe."

We see in these examples cosmologists seeming to act according to a principle like this: "If what you have directly observed cannot credibly account for what we see in nature, then be willing to postulate some very important mysterious invisible reality that cannot be directly observed."  But neuroscientists refuse to follow such a principle. Nature gives us innumerable examples of mental phenomena that cannot be credibly explained by brains (phenomena discussed in the posts of this blog). But rather than intelligently postulating some mysterious reality beyond the brain, our neuroscientists just keep senselessly claiming that the brain explains everything. 

But what if neuroscientists were to act according to the same principle quoted above? Then we might read a conversation something like the imaginary conversation below:

Science journalist: We are here with Professor Smith, and I will ask him about his interesting theory of a "dark brain." Professor Smith, what is this "dark brain" that you postulate?

Professor Smith:  What I call the dark brain is a mysterious invisible reality that must exist in each of our bodies, in addition to our visible brains. I believe that the dark brain is made of some kind of matter or energy that we cannot directly observe. 

Science journalist: Why do we need to postulate such a "dark brain"? Why can't we just assume that there only exists the regular physical brain that doctors see when they open up someone's skull?

Professor Smith:  There are all kinds of powerful reasons. One reason is that the known physical brain cannot account for memory formation and memory persistence. Humans can remember things very well for fifty or sixty years, but there's nothing in the known physical brain that can account for that.  The reigning theory is that memories are stored in synapses, but that's ridiculous, because the proteins in synapses only last for a few weeks, and synapses are attached to dendritic spines that don't last for years. There's also nothing in the known physical brain that can account for instant memory formation. Don't tell me that's "synapse strengthening," which would take minutes or hours. We've examined synapses with the most powerful microscopes. No one has ever found a human memory by microscopically observing synapses or any part of the physical brain. We can't even find any information storage code in the known physical brain, outside of the genetic code used by the DNA of all cells, which only has chemical information, not conceptual or memory information. 

Science journalist: But at least the known physical brain can explain memory recall, right?

Professor Smith:  Not at all.  Humans can recall complex learned information instantly, given a single word. For example, if you say "Waterloo," I may instantly say "A battle in 1815 in which Napoleon Bonaparte suffered his final military defeat." But how could I retrieve such information instantly, using a visible physical brain lacking any of the things that make instant information recall possible? It would be like finding a needle in a haystack. We know from our work with computers the kind of things that a system needs to be able to instantly retrieve information: things like addressing, sorting and indexing. No such things exist in the visible physical brain. 

Science journalist: So if we imagine this "dark brain" we can account for some things that the known physical brain cannot explain?

Professor Smith:  Yes, exactly. There are all kinds of other things we observe that we cannot explain with the mere idea of the known  physical brain. Consider out-of-body experiences. People often report floating out of their bodies and observing their bodies from above such bodies, particularly during near-death experiences. There's no credible way to account for that using a physical brain trapped in your skull.  But you can account for it assuming that someone's invisible dark brain can leave his body.  Then there's the well-documented reality of ESP. You can't account for extrasensory perception with the known physical brain. But such a thing could be possible if we each have an invisible dark brain that has powers and limits we don't understand. 

Science journalist: So has someone photographed such a "dark brain"?

Professor Smith:  No, presumably because it's made of some kind of energy or matter we can't currently measure or photograph with our current instruments.

Science journalist: But is it scientific to postulate some important causal reality is invisible?

Professor Smith:  Of course it is. That's what cosmologists and astrophysicists do constantly.  Such scientists are always appealing to some invisible and mysterious "dark matter" and "dark energy" to account for things they can't explain. If cosmologists and astrophysicists can do that, why can't neuroscientists do something very similar, by postulating a dark brain that is not directly observable?

Science journalist: But what could be the cause of such a "dark brain"?

Professor Smith:  We don't know. There could conceivably be some natural cause of dark brains.  But if there was a natural cause, dark brains would have to have originated through some way unlike anything evolutionary biologists or developmental biologists understand. 

The imaginary Professor Smith might have great success in advancing such a theory, just as long as he kept using this term "dark brain" and avoided using the term "soul" or "spirit," which would mean basically the same thing.  Neuroscientists might well be willing to believe in something exactly the same as what the common person understands under the names of "soul" or "spirit," as long as such a thing was described using the term "dark brain." But neuroscientists senselessly refuse to believe in such a thing (despite so many reasons for believing in it) as long as someone uses the terms "soul" or "spirit." It's like there is a tribal taboo that neuroscientists are committed to, one that unreasonably forbids them from using the words "soul" or "spirit."

The US Government's False Claims About DNA

What I call the Great DNA Myth is a false teaching that continues to be spread by innumerable parties in the world of biology, even though there are very many other authorities in that same world who are telling us the teaching is false.  The Great DNA Myth is the myth that inside DNA is some blueprint or recipe that specifies how to make a human body.  

There are various ways in which this false idea is stated, all equally false:

• Someone may describe DNA or the genome as a blueprint for an organism.
• Someone may describe DNA or the genome as a recipe for making an organism.
• Someone may describe DNA or the genome as a program for building an organism.
• Someone may claim that DNA or genomes specify the anatomy of an organism. 
• Someone may claim that genotypes (the DNA in organisms) specify phenotypes (the observable characteristics of an organism).
• Someone may claim that genotypes (the DNA in organisms) "map"  phenotypes (the observable characteristics of an organism) or "map to" phenotypes.
• Someone may claim that DNA contains "all the instructions needed to make an organism."
• Someone may claim that there is a "genetic architecture" for an organism's body or some fraction of that body. 
• Using a little equation, someone may claim that a "genotype plus the environment equals the phenotype," a formulation as false  as the preceding statements, since we know of nothing in the environment that would cause phenotypes to arise from genotypes that do not specify such phenotypes. 

Weaker formulations of this false idea include claims that DNA is "life's instruction book" or "the key to life" or "the book of life" or "the secret of life." While such rather vague assertions are not as explicitly false as the statements in the bullet list above, such formulations are equally misleading, as they insinuate the false claims in such a bullet list. Variations on these false statements above may use the term "genes" rather than DNA or genome. Such statements are equivalent to the statements above, because a gene is merely part of DNA (human DNA consists of roughly 20,000 genes). 

There is no truth to the claim that DNA is a specification for anatomy.  DNA merely specifies low-level chemical information such as which sequences of amino acids make up polypeptide chains that are the starting points of protein molecules.  Many biology authorities (some of which I quote below) have confessed this reality that DNA does not specify anatomy. But the "useful stooge" that is the Great DNA Myth continues to be taught or suggested in the literature of biology by many other people.  So now we have a very strange situation that might be described like this: biology's left hand is writing one thing, and biology's right hand is writing the opposite.  

The US Government's Fictions About DNA

False claims about DNA are found not only in the literature of many biologists, but in some of the official proclamations of the US federal government. Examples can be found at the government site www.genome.gov. Below are some examples:

(1) At the government page here (https://www.genome.gov/about-genomics/about-genomics/educational-resources/infographics/Your-Genome-You) we are incorrectly told "The genome contains all the instructions for you to grow throughout your lifetime."  This is not true. A genome (a person's DNA) merely specifies low-level chemical information, and does not specify how the progression from a tiny speck-sized zygote to a full adult body can occur. No instructions on how to build a human body are found in DNA, which does not even specify how to make any of the roughly 200 types of cells in the human body. 

(2) The US government page here (https://www.genome.gov/about-genomics/fact-sheets/Deoxyribonucleic-Acid-Fact-Sheet) misleadingly states that "the complete DNA instruction book, or genome, for a human contains about 3 billion bases and about 20,000 genes on 23 pairs of chromosomes." In this sentence DNA is referred to as if it an instruction book for making a human. DNA is no such thing. All it contains is low-level chemical information, such as which amino acids make up particular proteins.  The same page misleads us when it states this: "DNA contains the instructions needed for an organism to develop, survive and reproduce." DNA does have any instructions for how a full human body can develop from a speck-sized fertilized zygote, and DNA does not tell us anything about what we need to survive or reproduce. 

(3) Another US government page (https://www.genome.gov/about-genomics/fact-sheets/A-Brief-Guide-to-Genomics) here falsely tells us that "Deoxyribonucleic acid (DNA) is the chemical compound that contains the instructions needed to develop and direct the activities of nearly all living organisms." DNA does not have instructions specifying the anatomical organization of a human, and does not "direct the activities of nearly all living organisms." DNA lists the structure of some chemicals you need; it does not direct your activities. The same page contains the untrue claim that "DNA contains the information needed to build the entire human body." DNA does not specify any anatomical structures in a human, and does not even specify how to make any of the 200 types of cells in they human body. The same page makes the extremely absurd claim that "virtually every human ailment has some basis in our genes." For example, when you get pneumonia or influenza or COVID-19 or many infectious diseases, you have got an ailment that does not have any basis in your genes. And when you are injured in an accident, that has no basis in your genes.  

(4) On the page here (https://www.genome.gov/About-Genomics/Introduction-to-Genomics) we get the false claim that "Each genome contains the information needed to build and maintain that organism throughout its life."  Genomes (DNA molecules) contain no instructions on how to build an organism or any of its cells. The rest of the page contains some equally misleading misinformation. 

(5) The title of the NASA web page here (https://www.nasa.gov/feature/goddard/2022/life-blueprint-in-asteroids) refers to DNA as "the blueprint for life."  The page makes the very untrue claim that DNA  "contains the instructions to build and operate every living being on Earth."  

(6) On the US government page here (https://www.genome.gov/outreach/unlocking-lifes-code-exhibition#) we are given a link to the video at https://www.youtube.com/watch?v=kEJ0eRaebIc (here). At the beginning of that video, we have a young boy say, "I have always found it really intriguing that everything about who we are and what we look like is controlled by these tiny molecules called DNA." This extremely false statement is not corrected, just as if the makers of the video wanted you to believe it is true. 

A misleading visual on a US government web page

Some Experts Who Told Us the Truth About DNA

Below are some quotes by distinguished biology authorities revealing how false is the US government misinformation about DNA quoted above.

In this .pdf file, a professor of Mathematical Biology makes this statement:

"Although genes obviously play a role in development, knowing the genetic make-up of an organism does not allow us to understand the mechanisms of development—we may know that certain genes impart particular properties to certain cells, but how this then leads to tissue-level behaviour cannot be addressed by genetics."

That is basically a fancy way of saying that a fertilized egg does not become a baby by following a body plan stored in DNA. 

On page 26 of the book The Developing Genome, Professor David S. Moore states, "The common belief that there are things inside of us that constitute a set of instructions for building bodies and minds -- things that are analogous to 'blueprints' or 'recipes' -- is undoubtedly false." The same expert (in a paper claiming massive misuse by others of the term "heritability") states, "Our DNA, we now know, does not contain specific blueprint-like instructions about traits." 

Biologist Rupert Sheldrake says this about this issue:

"DNA only codes for the materials from which the body is constructed: the enzymes, the structural proteins, and so forth. There is no evidence that it also codes for the plan, the form, the morphology of the body. To see this more clearly, think of your arms and legs. The form of the arms and legs is different; it's obvious that they have a different shape from each other. Yet the chemicals in the arms and legs are identical. The muscles are the same, the nerve cells are the same, the skin cells are the same, and the DNA is the same in all the cells of the arms and legs. In fact, the DNA is the same in all the cells of the body. DNA alone cannot explain the difference in form; something else is necessary to explain form."

An evolutionary biologist notes that "the long-held belief that genes are the unique determinants of biological form in development and evolution has been challenged by an extensive number of commentators."  Among these "extensive number of commentators" are the people mentioned above and the authors of this scientific paper, who note that "gene expression patterns cannot explain the development of the precise geometry of an organism and its parts in space."

Describing conclusions of biologist Brian Goodwin, the New York Times says, "While genes may help produce the proteins that make the skeleton or the glue, they do not determine the shape and form of an embryo or an organism." Massimo Pigliucci (mainstream author of numerous scientific papers on evolution) has stated  that "old-fashioned metaphors like genetic blueprint and genetic programme are not only woefully inadequate but positively misleading." Neuroscientist Romain Brette states, "The genome does not encode much except for amino acids."

In a 2016 scientific paper, three scientists state the following:

"It is now clear that the genome does not directly program the organism; the computer program metaphor has misled us...The genome does not function as a master plan or computer program for controlling the organism; the genome is the organism's servant, not its master....Metaphorically, we can think of the genome as akin to a list of words, a vocabulary, which can be used to build and express a meaningful language; like a vocabulary, a genome by itself has no functional meaning. The genome is thus akin to a toolbox of DNA sequences that provide molecular tools as requested by the internal state of the organism and the state of the environment. One's genes cannot explain one's being: an organism is the expression of a dynamic and ongoing interaction between the state of its environment and its internal state, which includes its past history and its toolbox of DNA sequences."

In the book Mind in Life by Evan Thompson (published by the Belknap Press of Harvard University Press) we read the following on page 180: "The plain truth is that DNA is not a program for building organisms, as several authors have shown in detail (Keller 2000, Lewontin 1993, Moss 2003)." C.H. Waddington is described by wikipedia.org as "a British developmental biologist, paleontologist, geneticist, embryologistand philosopher who laid the foundations for systems biology, epigenetics, and evolutionary developmental biology."  He stated, "The DNA is not a program or sequentially accessed control over the behavior of the cell." Scientist Jean Krivine presents here a very elaborate visual presentation with the title, "Epigenetics, Aging and Symmetry or why DNA is not a program." Scientists Walker and Davies state this in a scientific paper:

"DNA is not a blueprint for an organism; no information is actively processed by DNA alone. Rather, DNA is a passive repository for transcription of stored data into RNA, some (but by no means all) of which goes on to be translated into proteins."

Geneticist Adam Rutherford states that "DNA is not a blueprint," a statement also made by biochemistry professor Keith Fox.  A press account of the thought of geneticist Sir Alec Jeffreys states, "DNA is not a blueprint, he says."  B.N. Queenan (the Executive Director of Research at the NSF-Simons Center for Mathematical & Statistical Analysis of Biology at Harvard University) tells us this:

"DNA is not a blueprint. A blueprint faithfully maps out each part of an envisioned structure. Unlike a battleship or a building, our bodies and minds are not static structures constructed to specification."

"The genome is not a blueprint," says Kevin Mitchell, a geneticist and neuroscientist at Trinity College Dublin. "It doesn't encode some specific outcome."  His statement was reiterated by another scientist. "DNA cannot be seen as the 'blueprint' for life," says Antony Jose, associate professor of cell biology and molecular genetics at the University of Maryland. He says, "It is at best an overlapping and potentially scrambled list of ingredients that is used differently by different cells at different times."  Sergio Pistoi (a science writer with a PhD in molecular biology) tells us, "DNA is not a blueprint," and tells us, "We do not inherit specific instructions on how to build a cell or an organ." Michael Levin (director of a large biology research lab) states that "genomes are not a blueprint for anatomy," and after referring to a "deep puzzle" of how biological forms arise, he gives this example: "Scientists really don’t know what determines the intricate shape and structure of the flatworm’s head."

Agustin Fuentes, a professor of anthropology, states the following:

"Genes play an important role in our development and functioning, not as directors but as parts of a complex system. 'Blueprints' is a poor way to describe genes. It is misleading to talk about genes as doing things by themselves."

On the web site of the well-known biologist Denis Noble, we read that "the whole idea that genes contain the recipe or the program of life is absurd, according to Noble," and that we should understand DNA "not so much as a recipe or a program, but rather as a database that is used by the tissues and organs in order to make the proteins which they need." 

In statements such as this, scientists "fess up" that the idea of DNA as a human specification is not true. Two other scientists "fess up" in a similar way when they write the following about genes in the journal Nature: "Population genetics is founded on a subset of coding sequences that can be related to phenotype in a statistical sense, but not based on causation or a viable causal mechanism."

Regarding the DNA as blueprint idea wikipedia.org article entitled “Common misunderstanding of genetics” lists the claim that “Genes are a blueprint of an organism's form and behavior” as one of the “common misunderstandings of genetics.” Jonathan Latham has a master's degree in Crop Genetics and a PhD in virology. In his essay “Genetics Is Giving Way to a New Science of Life,” a long essay well worth a read, Latham exposes many of the myths about DNA being a blueprint or master controller, and points out DNA does not even fully specify a protein. He states, "It is habitually, but lazily, presumed that DNA specifies all the information necessary for the formation of a protein, but that is not true." 

Ian Stevenson M.D. cited quite a few biologists pointing out the genes and DNA cannot determine the form of an organism:

"Genes alone - which provide instructions for the production of amino acids and proteins -- cannot explain how the proteins produced by their instructions come to have the shape they develop and, ultimately, determine the form of the organisms where they are. Biologists who have drawn attention to this important gap in our knowledge of form have not been a grouping of mediocrities (Denton, 1986; Goldschmidt, 1952; B. C. Goodwin, 1985, 1988, 1989, 1994; Gottlieb, 1992; Grasse, 1973; E. S. Russell...Sheldrake, 1981; Tauber and Sarkar, 1992; Thompson, 1917/1942)."

Biologist B.C. Goodwin stated this in 1989: "Since genes make molecules, genetics...does not tell us how the molecules are organized into the dynamic, organized process that is the living organism."  A paper by Stuart A. Newman (a professor of cell biology and anatomy) discussing at length the work of scientists trying to evoke "self-organization" as an explanation for morphogenesis states that "public lectures by principals of the field contain confidently asserted, but similarly oversimplified or misleading treatments," and says that "these analogies...give the false impression that there has been more progress in understanding embryonic development than there truly has been." Referring to scientists moving from one bunk explanation of morphogenesis to another bunk explanation for it, the paper concludes by stating, "It would be unfortunate if we find ourselves having emerged from a period of misconceived genetic program metaphors only to land in a brave new world captivated by equally misguided ones about self-organization."

Referring to claims there is a program for building organisms in DNA, biochemist F. M. Harold stated "reflection on the findings with morphologically aberrant mutants suggests that the metaphor of a genetic program is misleading." Referring to  self-organization (a vague phrase sometimes used to try to explain morphogenesis), he says, "self-organization remains nearly as mysterious as it was a century ago, a subject in search of a paradigm." 

Physician James Le Fanu states the following:

"The genome projects were predicated on the reasonable assumption that spelling out the full sequence of genes would reveal the distinctive genetic instructions that determine the diverse forms of life. Biologists were thus understandably disconcerted to discover that precisely the reverse is the case. Contrary to all expectations, there is a near equivalence of 20,000 genes across the vast spectrum of organismic complexity, from a millimetre-long worm to ourselves. It was no less disconcerting to learn that the human genome is virtually interchangeable with that of both the mouse and our primate cousins...There is in short nothing in the genomes of fly and man to explain why the fly has six legs, a pair of wings and a dot-sized brain and that we should have two arms, two legs and a mind capable of comprehending the history of our universe."

The false claim that DNA is a blueprint or recipe for making a human was denounced by Ken Richardson, formerly Senior Lecturer in Human Development at the Open University. In an article in the mainstream Nautilus science site, Richardson stated the following:

"Scientists now understand that the information in the DNA code can only serve as a template for a protein. It cannot possibly serve as instructions for the more complex task of putting the proteins together into a fully functioning being, no more than the characters on a typewriter can produce a story."

Writing in the leading journal Cell, biologists  Marc Kirschner, John Gerhart and Tim Mitchison stated, "The genotype, however deeply we analyze it, cannot be predictive of the actual phenotype, but can only provide knowledge of the universe of possible phenotypes." That's equivalent to saying that DNA does not specify visible biological structures, but merely limits what structure an organism can have (just as a building parts list merely limits what structures can be made from the set of parts). A paper co-authored by a chemistry professor (Jesper Hoffmeyer) tells us this: "Ontogenetic 'information,' whether about the structure of the organism or about its behavior, does not exist as such in the genes or in the environment, but is constructed in a given developmental context, as critically emphasized, for example, by Lewontin (1982) and Oyama (1985)." A paper by Stuart A. Newman (a professor of cell biology and anatomy) refers to "misconceived genetic program metaphors." 

At the Biology Stack Exchange expert answers site, someone posted a question asking which parts of a genome specify how to make a cell (he wanted to write a program that would sketch out a cell based on DNA inputs).  An unidentified expert stated that it is "not correct" that DNA is a blueprint that describes an organism, and stated that "DNA is not a blueprint because DNA does not have instructions for how to build a cell." No one contradicted this person's claim, even though the site allows any of its experts to reply. "DNA is not a blueprint for an organism," states Templeton Prize-winning physicist and astrobiologist P. C. W. Davies. On page 26 of his book Biology as Ideology: The Doctrine of DNA, biologist Richard C. Lewontin stated this:

"We are not determined by our genes, although surely we are influenced by them...Even if I knew the complete molecular specification of every gene in an organism, I could not predict what that organism would be....Even if I knew the genes of a developing organism and the complete sequence of its environments, I could not specify that organism."

The same biologist on page 52 mentions only one of several reasons that can help explain why so many misstatements have been made about DNA, stating this: "Among molecular biologists who are professors in universities, a large proportion are also principal scientists or principal stockholders in biotechnology companies." 

Why DNA as Body Blueprint Is a Childish Absurdity

If you ponder the simple fact that blueprints don't build things, you can start to get an idea of how nonsensical and childish is the claim that a human arises because a DNA blueprint is read.  Blueprints have no power of construction.  When buildings are built with the help of blueprints, it is because intelligent agents read the blueprints to get an idea of what type of construction work to do, and because intelligent agents then follow such instructions. But there is nothing in the human body below the neck with the power to understand and carry out instructions for building a body if they happened to exist in DNA. 

Consider what goes on when you read a web page at a complicated site such as www.facebook.com or www.buzzfeed.com.  What occurs is a very complicated interaction between two things: (1) a web page that is rather like a blueprint for how the page should look and act, and (2) an extremely complicated piece of software called a web browser, which is rather like a construction crew that reads the web's page blueprint (typically written in HTML), and then constructs very quickly a well-performing web page.  If the web browser did not exist, you would never be able to get a well-performing web page.  The construction of a three-dimensional human body would be a feat trillions of times more complicated than the mere display of a two-dimensional web page.  Just as it is never enough to have just a web page without a web browser,  having some DNA blueprint for building a body would never be enough to build a body.  You would also need to have some "body blueprint reader/body construction system" that would be some system almost infinitely more complicated than a web browser, in order for a body to get built from a DNA blueprint if it existed.  

We have no evidence that DNA contains any instructions for building cells or anatomy, and we also have no evidence for the existence of any such thing as a "body blueprint reader" in the human body, capable of reading, understanding and executing incredibly complicated instructions for building a human body. When you consider the amount of organization in a human body, you may start to realize the gigantic absurdity of thinking that a human specification can be found in some molecule merely listing low-level chemical information. 

Instead of being written using some kind of coding system allowing unlimited expression, DNA is written in the coding system of what is called the genetic code, which is shown below. Such a system allows only the narrowest type of expression: the mere specification of amino acids, low-level chemical building blocks. We see below how this genetic code works.  The letters A, T, C and G represent particular types of nucleotide base pair combinations in DNA. 

The organization of large organisms is extremely hierarchical.  Subatomic particles are organized into atoms, which are organized into amino acids, which are organized into protein molecules, which are organized into protein complexes, which are organized into organelles, which are organized into cells, which are organized into tissues, which are organized into organs, which are organized into organ systems, which are organized into organisms. 

Cells are so complex they have been compared to cities. The diagrams you see of cells are enormously misleading, making them seem a thousand times simpler than they are.  A cell diagram will show 20 or 30 organelles in a cell, but the actual number is typically more than 1000.  A cell diagram will typically depict a cell as having only a few mitochondria, but cells typically have many thousands of mitochondria, as many as a million. A cell diagram will typically depict a cell as having only a few lysosomes, but cells typically have hundreds of lysosomes. A cell diagram will typically depict one or a few stacks of a Golgi appartus, each with only a few cisternae, but a cell will typically have between 10 and 20 stacks, each having as many as 60 cisternae.  There are about 200 different cells in the human body. 

Internally organisms are enormously dynamic, because of constant motion inside the body, the incredibly complex choreography of metabolism, and also because of a constant activity inside the body involving cellular changes. Just one example of this enormously dynamic acitvity is the fact that protein molecules in the brain are replaced at a rate of about 3% per day. A large organism is like some building that is constantly being rebuilt, with some fraction of it being torn down every day, and some other fraction of it being replaced every day.  The analogy comparing a cell to a factory gives us some idea of the gigantically dynamic nature of organisms.

When we consider this enormously dynamic complexity, you may realize that the very idea of a blueprint for building a body is an absurdity, like imagining that the choreography of all of this year's ballets and Broadway shows could be expressed in a blueprint. To have a visual specification for building a human body, you would need something more like a multi-volume set of manuals containing a total of thousands of pages filled with color diagrams and tons of fine print.  Even if such a specification existed in the human body, it wouldn't explain morphogenesis: because the specification would be so complex it would require some super-genius to understand it all and build things according to so complicated a specification. 

The development of a human body from a one-cell speck-sized zygote can properly be described as a four-dimensional affair. It involves creating a three-dimensional physical structure, but also a structure that is so enormously dynamic that there is very much the time element involved everywhere. Time is often described as the fourth dimension. Specifying the physical progression of a human (with an enormous degree of internal dynamism) from a one-celled zygote requires four dimensions of information, something unavailable in the mere one-dimensional information that is the string-like sequence of DNA.  As biologist Steven Rose has stated, "DNA is not a blueprint, and the four dimensions of life (three of space, one of time) cannot be read off from its one-dimensional strand."

So how does a full-sized human body manage to arise from the tiny barely visible simplicity of a speck-sized fertilized egg existing just after human conception? This is a miracle of origination a thousand miles over the heads of today's scientists, who lack any credible explanation for the origin of any adult human body. 

Philosophy of Mind Implications of the Limits of DNA and Misstatements About DNA

What I have discussed here demonstrates some things extremely relevant to the philosophy of mind:

(1) Leading biology authorities may teach some childish falsehood, brazenly speaking as if the groundless idea was fact. 

(2) This falsehood taught may be not merely some unproven idea, but an idea that is simply disproven and debunked by the known facts. 

If this can happen in regard to DNA, it can happen in regard to brains.  Just as many biology authorities routinely make claims about DNA contrary to known facts, many biology authorities make claims  about brains contrary to known facts, such as the claim that memories are stored by synapse strengthening, an idea violently contrary to what we know about synapses and the unstable dendritic spines they are attached to: their structural instability, the short lifetimes of their proteins (merely weeks or days), and the complete lack of any known thing in a synapse resembling an information storage system or an information storage code. Humans can remember things for 1000 times longer than the average lifetime of the proteins in synapses, and humans can form complex new memories instantly (much faster than the many minutes or hours needed to strengthen synapses). 

The fact that DNA fails to explain morphogenesis is of the greatest importance to the philosophy of mind. The failure of scientists to explain the physical origin of any human body suggests some great undiscovered causal reality helping to cause (in a top-down manner) the enormously impressive progression from a speck-sized zygote to the vast organization of the human body. If such a causal reality exists on the physical side, it then seems very reasonable to postulate such a causal reality existing on the mental side, helping to explain the origin of our minds and the preservation of our memories, not credibly explained by brain activity. For further explanation of this hypothesis of a top-down origin of the human mind, read my two posts here. 

Postscript: In the Guardian, science writer Phillip Ball says this about the Human Genome Project that ended in 2003:

"But a blizzard of misleading rhetoric surrounded the project, contributing to the widespread and sometimes dangerous misunderstandings about genes that now bedevils the genomic age.So far, there have been few attempts to set the record straight. Even now, the National Human Genome Research Institute calls the HGP an effort to read 'nature’s complete genetic blueprint for building a human being' – the 'book of instructions' that 'determine our particular traits'. A genome, says the institute, 'contains all of the information needed to build and maintain that organism'. But this deterministic 'instruction book' image is precisely the fallacy that genomics has overturned, and the information in the genome is demonstrably incomplete. Yet no one associated with genomic research seems bothered about correcting these false claims...Plenty remain happy to propagate the misleading idea that we are 'gene machines' and our DNA is our 'blueprint'.